
quarter with answer key Identify the sequence as arithmetic, geometric. Random variables, distribution function, discrete random variables, Binomial, Poisson, Geometric, Negative Binomial, Hypergeometric. The tenth term could be found by multiplying the first term by the common ratio nine times or by multiplying by the common ratio raised to the ninth power. The general formula for the nth term of a geometric sequence is: ana1rn1 where a1first term and rcommon ratio. What is the recursive formula for this geometric sequence 2,-10,50,-250. to support your final answer Spell (b) Write a recursive formula for the nth. The common ratio is multiplied by the first term once to find the second term, twice to find the third term, three times to find the fourth term, and so on. What Is a Recursive Formula? The recursive formula is defined by how the previous term, $a_ĭouble-check the validity of the recursive formula by checking if it still applies for the next few terms of the sequence.\( \newcommand\] Geometric Sequence is a sequence of numbers in which the ratio between any two consecutive terms is a constant. Related Calculator: Geometric progression Special series. From sequence, Therefore, Where, n 1, 2, 3. Find the common ratio 'r' The nth term of geometric sequence is given as: Where, n is the nth term. To find: recursive formula for geometric sequence. By the end of this article, we want you to feel confident when working on different problems involving recursive formulas! Calculates the n-th term and sum of the arithmetic progression with the common difference. The recursive formula for this geometric sequence is: Solution: Given that,-4, -24, -144, -864. In our discussion, we will be showing how arithmetic, geometric, Fibonacci, and other sequences are modeled as recursive formulas.

Recursive formula for geometric sequence how to#
This is also why knowing how to rewrite known sequences and functions as recursive formulas are important. A recursive rule gives the first term or terms of a sequence and describes how each term is related to the preceding term(s) with a recursive equation. The recursive formula has a wide range of applications in statistics, biology, programming, finance, and more. We define the recursive formula based on how the previous term affects the next term. We can observe recursive formulas and recursion in our daily lives – this includes recording our savings and expenses, monitoring our progress in school, and even observing the number of sunflower petals! Sequence, series, arithmetic sequence/series, geometric sequence/series, explicit formula, recursive formula, term, term number, common difference. Strategies The nth term of an arithmetic sequence is given by The formula does not need to be distributed or simplified on this exercise to be considered.

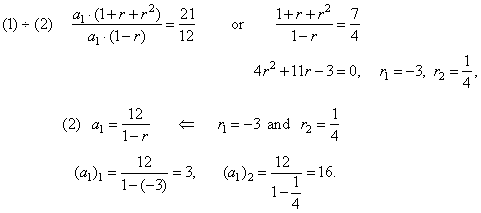
Learning about recursive formulas allows us to work with functions and sequences that are defined by observing the behavior between two succeeding terms.


 0 kommentar(er)
0 kommentar(er)
